A Reprogrammable Processor

for Fractal Image Compression

Barry Fagin

Department of Computer Science

United States Air Force Academy

2354 Fairchild Drive Suite 6K41

USAF Academy, Colorado 80840-6234 USA

Pichet Chintrakulchai

Thayer School of Engineering

Dartmouth College

Hanover, NH 03755-8000 USA

Abstract. Fractal image compression appears to be a good candidate for implementation with a reprogrammable processor. It is computationally intensive, slow on existing technology, and employs a few basic, well-defined functions that are clear candidates for hardware implementation. We discuss our implementation of a reconfigurable processor for fractal image compression, used to evaluate the utility of different compression methods faster than a software-only approach.

1 Introduction

Fractal image compression has recently been proposed as an alternative to JPEG and other compression techniques [1,2,3]. By identifying an appropriate set of affine transformations, images can be stored as mathematical functions which can then be iterated on an arbitrary initial data set to approximate the original image. The challenge is to construct the transformation set. Because the search space is large, fractal image compression is computationally intensive. Fractal image compression of a 128 x 128 color image can take over 4 hours on an RS/6000.

The long turnaround time for a software-only implementation enhances the difficulty of experimentation with different search and comparison functions. We require both 1) improved performance of frequently executed functions, and 2) the ability to evaluate different functions as candidates for use in fractal image compression. This suggests the use of a reconfigurable coprocessor.

2 Architecture

Our coprocessor system is designed to work with the Apple Power Macintosh computer using the NuBus interface [4], as shown in Figure 1:

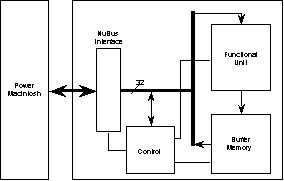
Fig. 1. Coprocessor Architecture

The coprocessor functions in either in compute mode or program mode. In program mode, the user feeds configuration data for a particular candidate function through the NuBus into the FPGAs. In compute mode, the host computer pumps input data through the NuBus which is then fed through the programmable functional unit. Output results are stored in the buffer memory. The functional unit is user-programmable and set up according to the directed acyclic graph (DAG) of the candidate operation. This DAG is the data flow pipeline of the candidate operation where many basic units can operate in parallel. Data dependency is the only limit for the degree of parallelism in each stage; results dependent upon the outputs of the current stage become the next stage of the pipeline. This way, we are able to exploit the parallelism both within a single stage of the pipe and across the entire pipeline where results are pumped out of the pipe every cycle after the pipe is filled.

3 Candidate Operation

Profile results gathered from running a fractal compression program on sample images on IBM RS6000/340 workstation show that the program spends more than 80% of total run time computing the absolute error between image blocks. This suggests that this function is a good candidate for hardware implementation.

Figure 2 shows the DAG for absolute error computation. Our calculations indicate implementation requirements of 123 CLB's and 64 I/O pins, easily within the limits of a Xilinx 4000-series FPGA [5]. Our results indicate that this routine can be sped up by approximately a factor of 50. Applying Amdahl's Law reduces the speedup to an approximate factor of 4, still a significant improvement. We are looking to incorporate other candidate functions into hardware, including genetic algorithms for searching the problem space and user-defined functions for determining similarity between portions of images.

This work was supported by the National Science Foundation under award # MIP - 9222643.

Fig. 2. DAG for 2x2 Pixel Error Computation

References

1. Barnsley, M.F. and Hurd, L.P., Fractal Image Compression, A.K. Peters, 1993.

2. Fisher, Y., Jacobs, E.W. and Boss, R.D., Fractal Image Compression using Iterated Transforms, Image and Text Compression, J. A. Storer Editor, Kluwer Academic Publishers, 1992.

3. Jacquin, A.E., Image Coding Based on a Fractal Theory of Iterated Contractive Image Transformations, IEEE Trans. on Image Processing, Vol. 1 (1), 1992, p. 18-30.

4. Apple Computer, Inc., Designing Cards and Drivers for the Macintosh Family (3rd Edition), Addison-Wesley, 1992

5. Xilinx Inc., The Programmable Logic Data Book, San Jose, CA, 1993.