Calculating the FHT in Hardware

Adam C. Erickson

Sequoia Systems Inc.

Marlboro, Massachusetts

{...seqp4!sequoia!adame}

Barry S. Fagin

Thayer School of Engineering

Dartmouth College

Hanover, NH 03755

603-646-3060

barry.fagin@dartmouth.edu

EDICS 4.11, 7.1.3, 7.2

ABSTRACT

We have developed a parallel, pipelined architecture for calculating the Fast Hartley Transform. Hardware implementation of the FHT introduces two challenges: retrograde indexing and data scaling. We propose a novel addressing scheme that permits the fast computation of FHT butterflies, and describe a hardware implementation of conditional block floating point scaling that reduces error due to data growth with little extra cost. Simulations reveal a processor capable of transforming a 1K-point sequence in 170 microseconds using a 15.4 MHz clock.

1.0 Introduction

The fast Hartley transform has attracted considerable research interest as an alternative to the FFT. A complete analogy exists between the two transforms. All the properties applicable to the FFT, such as the convolution and shifting theorems, apply to the FHT. In fact, the FHT is easily extracted from the real and imaginary components of the FFT (and vice versa). These properties have been well-documented in [Sore85], [Brac86], [Hou87], and [Onei88].

The computational advantage of the FHT lies in its use of real-valued data. As the vast majority of applications involve only real-valued data, significant performance gains are realized without much loss of generality. If one performs the complex FFT on an N-point real-valued sequence, the product is a complex sequence of 2N real points, N of which are redundant.^[1] The FHT, on the other hand, will yield a real sequence of the same length with no redundant terms, using only half the time and half the memory resources.

Real-valued FFT algorithms have been derived [Duha86, Sore87, Mou88] which compare in speed and memory requirements of the FHT, but they require the implementation of a different algorithm to compute the inverse real-valued FFT. This added complexity is undesirable, as algorithms for both the forward and inverse transform are preferred.

The FHT is obtained from the Discrete Hartley Transform (DHT) pair of a real function x(t), shown below:

⁽¹⁾

⁽²⁾

where cas(x) = cos(x) + sin(x). Note that the inverse DHT differs from the forward DHT only in a scaling factor, lending itself well to hardware implementation.

Like the DFT, naive implementations of the above equations imply O(N²) operations. Using techniques similar to the derivation of the FFT, the number of operations required to perform the DHT can be reduced to O(NlogN)^[2].

2.0 Previous Work

Hardware implementations of the FFT and similar algorithms fall into two categories: programmable DSP processors, and dedicated FFT processors. Most of those in the first class [Marr86], are extremely efficient when compared to general purpose Von Neumann architectures, but suffer in performance when compared with dedicated processors.^[3]

Academic efforts in dedicated FFT processors include a wafer-scale VLSI multiprocessor array capable of computing the FFT, proposed in [Kore81]. [Choi88] describes an extension of [Kore81] with improved fault tolerance, although performance figures are not reported. The CUSP dedicated-FFT processor [Lind85] has a very simple host interface and an elegant solution to controlling the overflow associated with fixed-point arithmetic. But the decision to implement bit-serial multipliers results in a single-processor system that is easily outperformed by ours and others [Shen88, Burs88].

One of the most successful commercial efforts in this area is Honeywell’s HDSP66110/220 chip-set [Shen88]. Capable of performing a 1024-point real-valued transform in 63 microseconds, this product combines a number of multiprocessing techniques to implement the fastest single-processor, radix-4 FFT engine known to the author. Several HDSP66110/220’s can be cascaded to gain even further performance, with a corresponding increase in cost.

Hardware realizations of the FHT are scarce. We conjecture that this is due not only to its relatively new stature in the ranks of fast algorithms, but also to the peculiar quirks of its implementation.

Software implementations of the FHT on Intel’s iPSC hypercube [Lin88] and the Connection Machine [Land90] have demonstrated that architectures of this type do not yet possess the interprocessor communication speeds necessary to compute the FHT efficiently. Here, 1K-point transform execution times are measured on the order of seconds. Adding processors can actually degrade performance, as communication overhead between the processors begins to offset any realized performance gains. Le-Ngoc and Vo offer another description of the implementation and performance of the FHT in [LENG89]. They publish estimated performance figures, of which only software implementations on the 80x86 microprocessor family reflect actual measurements. Estimates on other architectures are obtained by halving published FFT calculation times.

A summary of performance benchmarks for a number of general-purpose and dedicated-FFT processors is given in a later section. In the next section, we discuss the two principal challenges to hardware implementation of the FHT: retrograde-indexing and scaling.

3.0 The Challenges of Implementing the FHT

The two principal difficulties with implementing the FHT are retrograde indexing and data scaling. Retrograde indexing refers to the peculiar addressing pattern of the FHT, while scaling arises from our use of fixed-point arithmetic to calculate the FHT.

3.1 Retrograde Indexing

Addressing for the FHT exhibits a unique asymmetry. Figure 1 depicts the flow diagram for a decimation-in-time (DIT), radix-2, 16-point FHT [Kwon86]. Note the regular structure of the FHT. It is identical to a radix-2 FFT except for the ‘T’ blocks, which implement retrograde indexing. Visualizing larger transforms is straightforward: to construct a 32-point transform flow graph, we duplicate the 16-point transform diagram below for stages 1-4 and add a fifth stage with T5 in its lower half^[4].

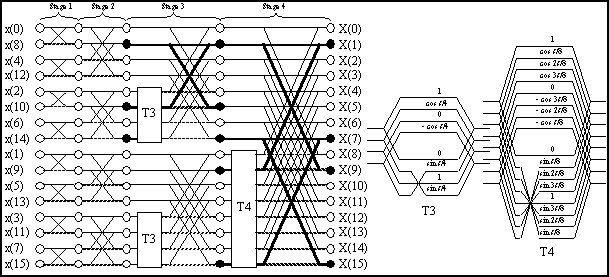Figure 1 Butterfly Diagram for 16-point FHT

[reproduced from [kwon86])

For the first two stages, FHT butterflies are similar to FFT butterflies, involving only two terms and no multiplications. For stage 3 and after, however, an increasing number of butterflies involve non-trivial multiplications. As T3 and T4 show, these butterflies require three input points to produce two output points (heavy lines, stage 3), introducing computational asymmetry and an I/O ratio of 3:2. The I/O efficiency can be improved by noting that two of the three terms used for any one butterfly are shared by a second butterfly in the same iteration. If the two associated butterflies are processed simultaneously, only four terms (not six) would be required (heavy lines, stage 4). Thus if we calculate two FHT butterflies at once, we may use four input points to calculate four output points, giving an I/O ratio of 1:1 [SORE85]. The concurrent calculation of two related butterflies will be referred to as a dual radix-2 butterfly. The equations of a dual radix-2 butterfly are shown below:

⁽³⁾

⁽⁴⁾

⁽⁵⁾

⁽⁶⁾

where i = 1,...,log₂N (stage counter), N_s = 2ⁱ (group size), f = 0,...,N_s/4 - 1 (butterflies within each group), and k = 0,N/N_s,...,(N/N_s - 1)*N/N_s (base index for each group). Whenever f evaluates to zero, Equations (3) - (6) are reduced to one addition or subtraction. This is the case for all of stages 1 and 2, half the butterflies in stage 3, and so on, decreasing to only 1 butterfly in the last stage. All the other butterflies involve general multiplication with the twiddle factors and two additions or subtractions. The next section discusses the consequences these operations can have on data integrity.

3.2 Preventing Overflow

Additions and subtractions using fixed-point arithmetic can result in data overflow, a situation which yields erroneous results and must be avoided during FHT calculation. In butterflies requiring three terms, two addition operations are involved. Studying Equations (3) - (6), we observe that the condition which results in the largest data growth is when f/N_s = 1/8 and the data are equal and at their maximum. Normalizing the maximum to be 1, the result of a worst-case computation is described by:

Because the result can grow by a factor of 2.4142, the data can experience up to élog₂2.4142ù = 2 bits of overflow. To prevent this, the data can be shifted right by two bits before performing the butterfly calculations. In addition to reducing the data’s dynamic range, this data scaling introduces truncation error if any of the discarded bits are non-zero. As the FHT calculations proceed from stage to stage and further data shifts are required, the error can propagate and grow enough to severely distort or completely obliterate the true output signal.

The technique used to scale the data can likewise degrade the signal-to-noise ratio. The easiest solution is to unconditionally shift the data right two bits at each stage. This would eliminate the possibility of overflow, at the cost of unnecessary shifting of data and a large loss of accuracy. Clearly other solutions are preferable.

Our processor implements a scaling technique known as conditional “block-floating-point” (BFP), whereby the data are shifted only when an overflow occurs [Welc69]. Instead of providing an exponent for each data word, as in floating-point, the entire sequence is associated with a single exponent. Should an overflow occur during an iteration, the entire array is shifted right by one and the exponent incremented.

How and when the sequence is shifted can effect system performance. [Welc69] suggests that the sequence be shifted immediately after an overflow. In this method, the sequence may be traversed twice during an iteration for the sole purpose of overflow adjustment. [ANDE88] limits the size of the incoming data to be two bits less than full-precision. The data are then allowed to grow into these extra bits during an iteration, after which an explicit subroutine is called to shift the sequence by the maximum amount of overflow that occurred. These schemes are not optimal because a significant portion of the FHT calculation is dedicated to adjusting the sequence. Our implementation improves upon existing methods by shifting the data as it arrives in the computational element during the next iteration, thereby precluding any time penalties. We discuss this in detail in a later section.

The situation resulting in the maximum possible bit growth arises when the input data are equal and at full-scale; that is, x(n) = [2^B-1-1,2^B-1-1,...,2^B-1-1] or [-2^B-1,-2^B-1,...,-2^B-1], where B is the processor’s word-length. The FHT of a constant input is an impulse whose amplitude is given by the following equation:

⁽⁷⁾

This result is intuitive, as a constant time-domain signal concentrates all its power into the DC component of its transform. Equation 7 shows that the data can grow by a factor of N, or log₂N bits, so when x is at full-scale, log₂N shifts are necessary to prevent overflow.

We note that the inverse transform would likewise produce log₂N bits of overflow given the same maximum DC input sequence. However, the inverse transform requires that we divide by N, equivalent to subtracting log₂N from the data’s common exponent. From equation 8, we see that the data, overall, does not experience any growth, although it experiences maximum data scaling. For a detailed analysis of this and other examples showing the effects of data scaling, the reader is referred to [ERIC90].

⁽⁸⁾

Knowing that a sequence can grow by one bit during the first two stages and by two bits in all subsequent stages, unconditional fixed-point scaling techniques would shift the data a total of 2log₂N - 2 bits, almost twice the maximum possible bit-growth. For this reason, block-floating-point schemes can generally be expected to perform better than unconditional schemes. Detailed error analyses for the fixed-point scaling techniques discussed here can be found in [welc69], [rabi73], and [oppe88]. A method of analysis specific to our implementation is presented in a later section.

4.0 Architecture of the FHT Processor

This section describes an architecture capable of computing the FHT very efficiently. For 1024-point transforms, 98 percent of the execution time is spent performing FHT calculations. We first discuss the system architecture, and then present solutions to the aforementioned implementation challenges.

4.1 System Architecture

The processor architecture embodies a number of techniques designed to optimize system performance and functionality. The butterfly computational unit (BCU) utilizes a 5-stage pipeline, keeping the critical path as short as possible. Additionally, the processor incorporates tightly-coupled, high speed buffer memories. Organized to hold up to 1024 16-bit words, each memory is arranged to allow simultaneous, single-cycle access to four 16-bit data points. Employing several of these memories allows for many such concurrent data transfers, boosting the data I/O rate significantly.

The processor can be programmed to transform sequence lengths of any power of two from 4 to 1024 points, thereby overcoming an inflexibility found in some dedicated hardware processors. Larger transforms are a simple extension of the processor’s address generation unit and an increase in the depth of the memories.

A block diagram of the system is given in Figure 2. The arithmetic element accepts four data elements (and the two sine and cosine terms) and outputs four processed elements every clock cycle. Each of the four buffer memories shown contains two independently addressable arrays 32 bits wide by 256 words deep. Two of these memories alternate as source and destination as the FHT calculations proceed from stage to stage. The other two memories not involved in the transform can be used to load newly-sampled data and unload recently processed data asynchronously while transform calculations of a third sequence are in progress, accommodating high-speed, real-time FHT processing.

Interface to a host machine is accommodated by 3 control lines and a 4-bit word indicating transform size which can easily be mapped into the host’s address space. To begin a transform, the host places the value log₂N on the data bus and asserts start. Calculations can be put on hold or halted altogether by asserting pause or reset, respectively. When a transform is complete, done is asserted. The host can then recover the processed data and their common exponent.

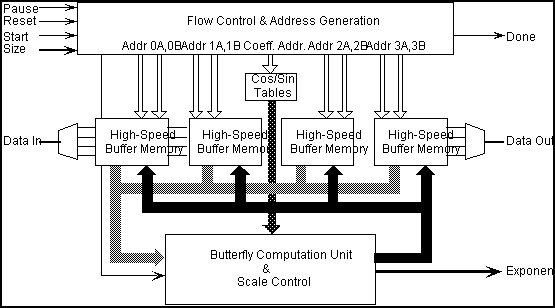
Figure 2 System Block Diagram

We have mentioned previously the two primary challenges to implementing the FHT: retrograde indexing and scaling. We now present our solutions to these problems.

4.2 Algorithm Control and Butterfly Computation

Because parallel access to all four elements of a dual radix-2 butterfly is desired, the processor employs an algorithm different from the one originally proposed in [Brac84]. Given a sequence of length 2^v, v Î [2,3,...,10], the sequence is broken into 4 equal segments and arranged as depicted in Figure 3. Each column in the array is a separate memory bank, where the first 1/4th of the sequence is loaded in the first bank, the second 1/4th in the second, and so on. Thus, a 16-point sequence would be stored as shown in Figure 3.

When calculations begin, the top data value from each of the memories can be fetched simultaneously (via memory address 0 being sent to all four memories), providing the BCU with the necessary data to calculate the first butterfly. Comparing Figures 1 and 3 will show that bit-reversal, an operation required before performing DIT butterfly calculations, is already partially accomplished (the destination addresses for the first stage will still need to be bit-reversed). A simple binary “butterfly” counter extending from 0 to N/4 - 1 can serve as the address to fetch the input data.

Figure 3 Arrangement of N-point Sequence into four separate memory banks

Once fetched, the data enter the Butterfly Computational Unit, pictured in Figure 4. The dotted lines in the figure show where clocked buffers are placed in order to implement the five-stage pipeline. Once the data arrive from memory, the data are first scaled according to the amount of overflow that occurred during the previous stage. Next, reordering of the data may be necessary due to the way data was written during the previous iteration. After reordering, the butterfly computations from equations (3) - (6) are performed. More post-calculation reordering may be necessary before the results are finally written to the destination memory.

As Figure 4 shows, butterfly calculation involves multipliers, adders and subtracters. Disposing of most of the subscripts and letting m denote the current stage number, Equations (3) - (6) simplify to:

A0_m+1 = A0_m + (B0_mcosq + B1_msinq) (9)

A1_m+1 = A1_m + (B1_mcosq - B0_msinq) (10)

B0_m+1 = A1_m - (B1_mcosq - B0_msinq) (11)

B1_m+1 = A0_m - (B0_mcosq + B1_msinq) (12)

These equations are similar to those used to calculate just one radix-2 complex FFT butterfly .

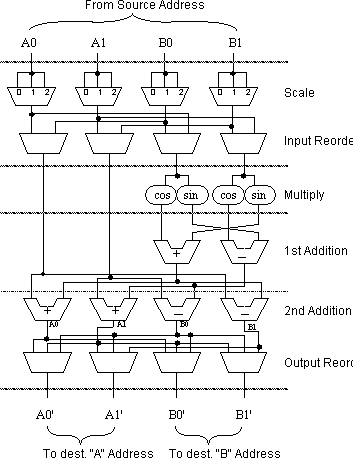
Figure 4 BCU Block Diagram

Although a sequence is stored in four separate memory banks, writing the results to the destination memory does not require the generation of four separate addresses. The BCU result data are written to the destination memory in pairs, requiring only two addresses, A and B (see Figure 4). Data must be written in this way to insure simultaneous access to four elements using a single source address during the next iteration.

4.3 Address Generation and Control

The correct computation of the FHT using the datapath of Figure 4 requires the specification of input and output reordering control signals. For some butterflies, the data emerging from the A and B sides of the pipeline must be swapped. This swapping must then be remembered by the processor during the next butterfly stage. Butterflies with 2 input points must also be handled differently.

Output and input reordering are indicated by the boolean variables O and I. These are used to re-route data coming from or going to the A or B memories, and are implemented as control signals in the processor. The i control line governs the reordering of data before a butterfly calculation. When the i control line is active in a given stage, the data coming from memory A is swapped with that of memory B. When o is active, the processed data to be written to memory A is swapped with that of memory B. If o is active for a butterfly in any stage, i will be active in the corresponding butterfly in the next stage.

The c control line accommodates butterflies requiring 2 (instead of 4) input terms. Note that in the first two stages c is always high. The BCU computes the correct results, but they are not in the proper order for writing out to memory. When c becomes active, results from the first adder and second subtracter (in the 2nd tier of ALUs) are written to destination memory A0 and A1, respectively, and results from the second adder and first subtracter are written to destination memory B0 and B1, respectively.

To analyze the operation of the control lines, it is convenient to number each butterfly with an address b, 0 <= b < N/4 - 1, where N is the input size, and to label the stages of the FHT with a number s, 0 <= s < log N. We divide the set of butterflies into groups of size 2^{s -1}, numbered from g = 0 .. N/2^{s + 1}-1 (if s = 0 the group size is defined to be 0). I, O, and C can then be specified as follows:

s = 0 I = 0, O = 1, C = 1

s = 1 I = 1, O = bit 0 of b , C = 1

s = 2 .. log N-2 I = bit s-2 of b , O = bit s-1 of b , C = NOR(lower s-1 bits of b )

s = logN - 1 I = bit s-2 of b , O = bit s-1 of b , C = 1

Bits are numbered from 0, and are assumed to be equal to zero if the indicated position is greater than logN - 3. Output reordering is always required for the first stage, and then for all the odd numbered groups. Input reordering is not required for butterflies in stage 0, but is needed at stage s for all butterflies with reordered outputs in the stage s-1. The C signal, for two-input butterflies, is always active during the first and second stages. C is then active for the first butterfly in each group until the last stage, when it is always asserted.

The destination A and B addresses of a butterfly b in group g for stage s can be specified in the following way:

IF s = 0

A := bit-reversed(b ), B := bit-reversed(b )

ELSE IF g is even

A := b

IF NOR(lower s-1 bits of b )

B := A plus 2^s-1

ELSE

B := 2^s (g+1) - A

ELSE

B := b

IF NOR(lower s-1 bits of b )

A := B plus 2^s-1

ELSE

A := 2^s (g +1) - B

For the first stage of the FHT, the A and B addresses are simply the bit-reversed equivalents of the butterfly addresses. Otherwise, for even groups A is the butterfly address. B is equal to A plus the group size if the butterfly is the first in a group, otherwise it is twice the group size times (g + 1 ) minus A. For odd groups, the A and B values are switched.

Our processor uses four memory banks, with two alternating as source and destination with each stage of the FHT. Alternatively, one may reduce system memory to two banks if special logic is added to stall the pipeline when the input and output stages attempt to access the same address. In a processor with k stages, this will occur when the destination address for butterfly b , is equal to b+k . It is not difficult to show that for k odd, accesses for s > 0 are conflict-free.

Destination addresses and control signal calculation for a 64-point FHT are shown in Table 1. This transform has 16 dual-radix butterflies. '•' denotes an asserted signal, 'b' a butterfly number, and 'g' a group number. A and B indicate A and B destination addresses, while I, O, and C denote the appropriate control signals. Groups are indicated by dotted lines.

b	g	I	C	O	A	B	g	I	C	O	A	B	g	I	C	O	A	B
0	-		•	•	0	0	0	•	•		0	1	0		•		0	2
1	-		•	•	8	8	1	•	•	•	1	0	0	•			1	3
2	-		•	•	4	4	2	•	•		2	3	1		•	•	2	0
3	-		•	•	12	12	3	•	•	•	3	2	1	•		•	3	1
4	-		•	•	2	2	4	•	•		4	5	2		•		4	6
5	-		•	•	10	10	5	•	•	•	5	4	2	•			5	7
6	-		•	•	6	6	6	•	•		6	7	3		•	•	6	4
7	-		•	•	14	14	7	•	•	•	7	6	3	•		•	7	5
8	-		•	•	1	1	8	•	•		8	9	4		•		8	10
9	-		•	•	9	9	9	•	•	•	9	8	4	•			9	11
10	-		•	•	5	5	10	•	•		10	11	5		•	•	10	8
11	-		•	•	13	13	11	•	•	•	11	10	5	•		•	11	9
12	-		•	•	3	3	12	•	•		12	13	6		•		12	14
13	-		•	•	11	11	13	•	•	•	13	12	6	•			13	15
14	-		•	•	7	7	14	•	•		14	15	7		•	•	14	12
15	-		•	•	15	15	15	•	•	•	15	14	7	•		•	15	13

stage 0 1 2

b	g	I	C	O	A	B	g	I	C	O	A	B	g	I	C	O	A	B
0	0		•		0	4	0		•		0	8	0		•		0	0
1	0				1	7	0				1	15	0		•		1	15
2	0	•			2	6	0				2	14	0		•		2	14
3	0	•			3	5	0				3	13	0		•		3	13
4	1		•	•	4	0	0	•			4	12	0		•		4	12
5	1			•	7	1	0	•			5	11	0		•		5	11
6	1	•		•	6	2	0	•			6	10	0		•		6	10
7	1	•		•	5	3	0	•			7	9	0		•		7	9
8	2		•		8	12	1		•	•	8	0	0	•	•		8	8
9	2				9	15	1			•	15	1	0	•	•		9	7
10	2	•			10	14	1			•	14	2	0	•	•		10	6
11	2	•			11	13	1			•	13	3	0	•	•		11	5
12	3		•	•	12	8	1	•		•	12	4	0	•	•		12	4
13	3			•	15	9	1	•		•	11	5	0	•	•		13	3
14	3	•		•	14	10	1	•		•	10	6	0	•	•		14	2
15	3	•		•	13	11	1	•		•	9	7	0	•	•		15	1

stage 3 4 5

Table 1: Address Generation and Control for 64-point FHT

4.4 An Example

Table 2 shows the addressing , control, and data values generated during the computation of a length-16 FHT. Note that there are log₂N =  4 stages, each with N/4 = 4 butterflies. In this example, we assign data points x[i] = i, for i = 0,...,N-1. Three views of the data are given as it is processed within the BCU. The box labelled “Memory” represents the contents of the source memory at the start of each iteration (and what arrives at the inputs to the BCU). Additionally, the butterfly results at the outputs of the second tier of adders is given, followed by the data after output reordering. Symbols used are similar to those in Table 1.

Stage 1

Memory 0 A 1 0 B 1	S	Dest A B	Control I C O	Before Output Reorder + + - -	Memory 0 A 1 0 B 1
0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15	0 1 2 3	0 0 2 2 1 1 3 3	• • • • • • • •	8 16 -8 -8 10 18 -8 -8 12 20 -8 -8 14 22 -8 -8	16 -8 8 -8 18 -8 10 -8 20 -8 12 -8 22 -8 14 -8
			Sta	ge 2
Memory 0 A 1 0 B 1	S	Dest A B	Control I C O	Before Output Reorder + + - -	Memory 0 A 1 0 B 1
16 -8 8 -8 20 -8 12 -8 18 -8 10 -8 22 -8 14 -8	0 1 2 3	0 1 1 0 2 3 3 2	• • • • • • • • • •	24 -16 0 -8 32 -16 0 -8 28 -16 0 -8 36 -16 0 -8	24 -8 -16 0 -16 0 32 -8 28 -8 -16 0 -16 0 36 -8
			Sta	ge 3
Memory 0 A 1 0 B 1	S	Dest A B	Control I C O	Before Output Reorder + + - -	Memory 0 A 1 0 B 1
24 -8 32 -8 -16 0 -16 0 28 -8 36 -8 -16 0 -16 0	0 1 2 3	0 2 1 3 2 0 3 1	• • • • • •	56 -16 0 -8 -27 11 -11 -5 64 -16 0 -8 -27 11 -11 -5	56 -8 -16 0 -27 11 -11 -5 -16 0 64 -8 -11 -5 -27 11
			Sta	ge 4
Memory 0 A 1 0 B 1	S	Dest A B	Control I C O	Before Output Reorder + + - -	Memory 0 A 1 0 B 1
56 -8 64 -8 -27 11 -27 11 -16 0 -16 0 -11 -5 -11 -5	0 1 2 3	0 0 1 3 2 2 3 1	• • • • • •	120 -16 0 -8 -48 31 -9 -6 -27 11 -11 -5 -20 3 -13 -2	120 -8 0 -16 -48 -6 31 -9 -27 -5 11 -11 -20 -2 3 -13
				¯
Final Sequence A B
120 -8 0 -16 -48 -6 3 -13 -27 -5 11 -11 -20 -2 31 -9

Table 2 Addressing and Data-Reordering Control for 16-point FHT

Figure 5 illustrates an example butterfly calculation. In the second butterfly of the second stage, the data [20, -8, 12, -8] are retrieved from the source memory. The I line is active for this butterfly, so the data are reordered as [12, -8, 20, -8]. Calculations on this data now proceed as described in equations (2.1) - (2.4) to produce [32, -16, 0, -8]. If no output reordering needs to be done, the data [32, -16] would get written to memory A and [0, -8] would get written to memory B. However, both c and o are active here. The c line causes the data to be reordered as [32, -8, -16, 0], and the o line, also being active, would subsequently swap the first two elements with the second two before releasing the data to memory. Thus, [32,-8] is written to location 0 of destination memory B, and [-16,0] is written to location 1 of destination memory A.

The three control lines, i, c and o, are wired to the input and output multiplexors in the BCU. The i line is wired directly to the 2-1 muxes at the inputs of the BCU, and the c and o lines are used to generate the data select lines for each of the four 3-1 output muxes.

A B

[ 20 -8 ][ 12 -8 ] Retrieve Data, addrA=addrB=1

[ 12 -8 20 -8 ] I Active: Swap A,B

[ 32 -16 0 -8 ] Perform Calculations

[ 32 -8 -16 0 ] C Active: A1=B1, B0=A1, B1=B0

[ -16 0 32 -8 ] O Active: Swap A with B

[ -16 0 ][ 32 -8 ] Write Data, addrA=1,addrB=0

Figure 5 Example Butterfly Illustrating the Operation of Address and Control Lines

We now turn our discussion to fixed-point versus floating-point arithmetic, pointing out the consequences of choosing one over the other.

4.5 Fixed-Point versus Floating-Point

Implementing a 16-bit fixed-point processor has important advantages over floating-point implementations. Standard, single-precision floating-point arithmetic operates on 32-bit data. This increased data width would have an enormous impact on the amount of hardware required to implement our processor. Memory width would double, as would all hardware used to compute the double radix-2 butterfly. Furthermore, to preclude any performance hits, additional pipeline hardware would be required to offset the higher latency of floating-point operations.

Floating-point hardware itself is relatively expensive. Not only is floating-point hardware functionally more complex than integer hardware, but, because of the larger data paths, the hardware must be housed in costly pin-grid-array packages. For these reasons, we felt that a fixed-point processor was better suited for our purposes.

In addition to aliasing, quantization, leakage and other sources of error inherent to discrete transform calculations, the fixed-point data will experience both roundoff and truncation error. Roundoff error is introduced at the multipliers, where only the 16 most-significant bits of the 32-bit product are used. In [zakh87], a theoretical analysis of fixed-point and floating point roundoff error is developed. The theoretical results are supported by subsequent experiments on white-noise input sequences. Given a zero-mean, white-noise, fixed-point input sequence, Zakhor found that the noise-to-signal ratio increases by about 1.1 bits per stage. This relatively high error can be partially attributed to her limiting the dynamic range of the input sequence in order to insure against overflow.

Truncation error occurs after an adder overflow, where the least-significant bit is shifted out.^[5] We attempt to minimize these effects by implementing block floating point scaling.

4.6 Block-Floating-Point Scaling

Among the components needed to implement BFP scaling are overflow-detection logic, a maximum-overflow register (maxovl) reflecting the largest growth (0, 1, or 2 bits) of data that occurred during the current stage, a scale register (scale), reflecting the largest growth of data that occurred during the previous stage, and the common exponent register (expo). Figure 6 illustrates their interconnection.

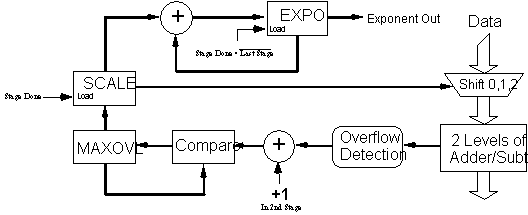
Figure 6 Scale Control Block Diagram

The input data are constrained to lie in the interval [-2¹⁴, 2¹⁴ - 1], leaving an extra bit available for the possible overflow in the first stage. The overflow occurring during each butterfly calculation is compared to maxovl, initialized to zero at the beginning of a each stage. If maxovl is exceeded, it is updated with the new maximum. At the end of the first stage, maxovl is stored into scale, added to expo, and then reset for the next stage.

As the data arrive during the second stage, they are scaled down by the value in scale before being processed. This will give back the extra bit needed to guard against a second-stage overflow.

Data during the third and later stages can experience two bits of overflow. Preparations for this occur during the second stage, where the overflow incurred during each butterfly calculation plus one is compared to maxovl. Thus, if no overflow occurs during the second stage, maxovl = 1. If an overflow does occur, maxovl = 2. In effect, an extra, unconditional shift is made to ensure that two guard bits are present for the third stage. A special case arises when none of the data occupies more than 14 bits of precision after the second stage. In this case, the two required guard bits are already present, and the unconditional shift does not take place.

Scale control at the end of the third and subsequent stages ensures that the data starts with two guard bits. This proceeds with no special cases until the last stage, where the data need not be adjusted after an overflow. Here, the data are allowed to grow to the full 16 bits of precision and are written to the output buffer memory unmodified.^[6] The exponent register will reflect the total amount of shifts the data underwent.

Everything said about the forward FHT applies equally as well to the inverse FHT; the only difference is that the exponent will be log₂N greater than the true value. A simple subtraction takes care of this.

Statistical models have been formulated which place an upper bound on the output noise-to-signal ratio for FFTs employing unconditional BFP scaling [welc69] and [oppe72]. Both authors assume that one bit of overflow occurs during each stage, and both obtain the same result, that the output noise-to-signal ratio increases by half a bit per stage. The output noise-to-signal ratio for conditional BFP scaling depends strongly on how many overflows occur, and at what points during the FFT calculation they occur. As the positions and timing of the overflows are correlated with the input signal, one needs to know the signal statistics in order to analyze the output noise-to-signal ratio. Instead of analyzing the problem theoretically, both authors perform experiments using white-noise inputs and compare the results to the upper bound obtained for unconditional BFP scaling. As expected, the experiments show that conditional BFP performed somewhat better than unconditional BFP, as fewer shifts of the data occurred, and hence less error propagated to the outputs.

We outline here a procedure similar to that used in [welc69] and [oppe71] for empirically determining the output signal-to-noise ratio for an FHT using conditional BFP scaling. We begin with an input sequence, x(n), and compute its FHT using two programs. The first program uses double-precision floating point in its FHT computations, which we take as exact. The second program emulates our FHT processor scale control hardware. Using fixed-point arithmetic, it will produce an output sequence equal to that of the first program plus an error sequence. The error sequence can be extracted by subtracting the outputs of the two programs, as shown below:

Figure 7 Procedure for BFP Scaling Error Analysis

The signal-to-noise ratio is determined by taking the ratio of the root-mean-square value of the floating-point sequence to that of the error sequence, where the RMS values are given by Equations (13) and (14). Note that the sequences’ mean values must be subtracted from each of the terms before being squared.

⁽¹³⁾

⁽¹⁴⁾

The results can be used to predict the SNR for several classes of input sequences and be compared to theoretical and experimental results for unconditional fixed-point implementations in [Oppe88] and [welc69]. An example calculation of the SNR for a maximum-amplitude, truncated cosine wave is provided in the Appendix.

5.0 Simulation of the Architecture and Performance Estimates

The two primary tools used to develop the FHT processor were the Workview^® design system, for schematic capture and simulation, and the XACT CAD package for gate array layout. Workview is an integrated schematic capture and simulation package; our version ran on a Sun 3/60 platform. XACT is a field programmable gate array die editor which gives the designer complete control over logic placement and routing resources. We have shown in [FAGI90] that user control at this level was essential to meeting our design spec of a 65ns clock period, corresponding to a 15.4 MHz system clock. For a more thorough description of the processor hardware, the reader is referred to [FAGI90] and [ERIC90].

5.1 Performance of the FHT Processor

Simulation has verified that we meet our system spec of a 65ns clock period. We may therefore calculate the performance of the FHT processor in the following way. There are log₂(N) stages in an N-point transform and N/4 dual-radix-2 butterflies in each stage. Given a throughput rate of one dual-radix-2 butterfly per clock cycle, the total number of cycles required to compute an N-point sequence is given by the relation (N/4+5)log₂(N)+3. The pipeline adds five cycles for each stage in the calculation, and three additional cycles are consumed to initiate the transform. With the system clock 15.4 MHz, a 1024-point transform can be performed in 170 mS, allowing one to perform real-time signal processing using a 6.04 MHz input sampling rate. Table 3 lists the various transform sizes and their execution times as given by the above equation.

Transform Size	Time to Complete
4	0.97 mS
8	1.56 mS
16	2.53 mS
32	4.42 mS
64	8.38 mS
128	17.01 mS
256	36.04 mS
512	77.92 mS
1024	169.68 mS

Table 3 Performance Benchmarks for FHT Processor

Table 4 compares our 1K-point benchmark with other implementations [LeNg89]. Most of the times given are one-half the time to calculate a 1K-point complex FFT, which is an accurate approximation to the time required to compute a 1K-point real transform. We limit our comparisons to DSP processors and chip sets, systems of comparable complexity to the FHT processor. More complex systems (for example [SWAR84] and [TMC89]) may exhibit improved performance, but at considerably increased cost.

Processor	Time to Calc. 1K-pt Transform	System Clock
Honeywell HDSP66110/66210	63 mS	25 MHz
FHT Processor	170 mS	15.4 MHz
TRW TMC2310	514 mS	20 MHz
CUSP	665 mS	50 MHz
Plessey PDSP 1600 Family	1000 mS	40 MHz
Texas Instruments TM320C30	1880 mS	16 MHz
Motorola MC56000	2500 mS	10 MHz
Phillips/Signetics DSP1	3430 mS	8 MHz
Advanced Micro Dev. ADSP-2100	3800 mS	8 MHz
NEC PD77230	5400 mS	6.7 MHz
Texas Instruments TM320C25	6600 mS	10 MHz
National Semiconductor LM32900	6700 mS	10 MHz

Table 4 Performance Comparison of Several DSP & Transform Processors

We caution against an unduly enthusiastic interpretation of Table 4. The reported time for the FHT processor is based on simulation, while other results are from functioning chips. Additionally, the FHT processor is a special purpose device, and should be expected to perform well on the chosen application when compared with more general purpose devices. Nonetheless, even when these factors are taken into account, we believe the performance difference to be significant.

6.0 Conclusions and Future Work

We have described a high-performance FHT architecture, discussing our solutions to the principal computational challenges of the FHT. Simulations reveal a processor capable of computing a real-valued, 1K-point transform in 170µS. The processor is among the fastest transform processors to date and is the only dedicated FHT hardware processor known to the authors.

The architecture has been fully simulated, and has up to this point met system specifications. The next step will include PCB fabrication and prototyping. While problems inevitably arise when constructing an experimental system, our previous experiences with the construction of digital systems under similar conditions have been quite successful [KUSK89]; we anticipate comparable results here. We note that the final design need perform only within 300% of specifications to offer superior performance to its closest rival.

Additional work should include the development of host interface to a standard bus with supporting software. We recommend the Nu-bus, Multibus, or VMEbus, as these are well-supported industry standards. If in addition support for direct loading of sequences via A/D converters is realized, the FHT processor could become an extremely powerful signal processing tool.

Our processor can easily be extended to support a number of DSP-related algorithms other than the FHT. General multiplication support for windowing and convolution applications requires little modification, as the multiplier hardware is already present. Multiplier-accumulation for FIR filtering and other iterative DSP applications could likewise be supported with little modification. In fact, it would not be too difficult to generalize the arithmetic element to accommodate the FFT and other transforms without loss of performance, as the BCU structure of the two algorithms are very similar. Given the flexibility reprogrammable gate arrays provide, the control unit could be reprogrammed dynamically to implement the FFT, FHT, or any other DSP-related algorithm without additional hardware. We propose this as a topic for future investigation.

7.0 Acknowledgements

The FHT processor was designed at the Thayer Rapid Prototyping Facility, a laboratory for the rapid production of high performance digital systems. Parts were ordered through the FAST parts broker, funded by the Department of Defense Advanced Research Projects Agency. We gratefully acknowledge Viewlogic Inc, for their provision and support of the Workview^® CAD package, and the Whitaker Foundation for their support of the Thayer RPF. Finally, the authors would like to thank Xilinx Incorporated for their support of software, equipment, and documentation.

8.0 Bibliography

[ANDE88] ANALOG DEVICES, ADSP-2100 Applications Handbook, Volume I, and ADSP 2100 User's Manual, 1988, Analog Devices, Signal Processing Division, One Technology Way, P.O. Box 9106, Norwood Mass., 02062.

[Blah85] Blahut, R., Fast Algorithms for Digital Signal Processing, Addison Wesley, 1985.

[Brac84] Bracewell, R. N., The Fast Hartley Transform, Proc. IEEE, Vol. 72, No. 8, August 1984.

[Brac86] Bracewell, R. N., The Hartley Transform, Oxford University Press, 1986.

[Brig88] Brigham, E. Oran, The Fast Fourier Transform and its Applications. Englewood Cliffs, New Jersey, Prentice Hall, Inc., 1988.

[Burs88] Bursky, D., One-Chip FFT Processor Rips Through Signal Data, Electronic Design, September 8, 1988, pp. 127-129.

[Choi88] Choi, Y. & Malek, M., A Fault-Tolerant FFT Processor, IEEE Transactions on Computers, Vol. 37 No. 5, pp 617-621, May 1988.

[Duha86] Duhamel, P., Implementation of “Split-Radix” FFT Algorithms for Complex, Real, and Real-Symmetric Data, IEEE Transactions on ASSP, Vol. 34, No. 2, April 1986.

[ERIC90] ERICKSON, A., A High Performance Processor to Compute the Fast Hartley Transform Using Field-Programmable Gate Arrays, Masters Thesis, Thayer School of Engineering, Dartmouth College, March 1990.

[FAGI90] FAGIN, B., Using Reprogrammable Gate Arrays in Performance Critical Designs, 3rd Microelectronics Conference, Santa Clara, CA 1990.

[Gane82] Ganesan, K., Govardhanarajan, T. S., Dhurkadas, A. & Veerabhadraiah, S., Hardware Realization of a General Purpose FFT Processor in a Distributed Processing Configuration, Defense Science Journal, Vol. 32, No. 1, January 1982, pp. 41-46.

[Gold73] Gold, B. & Bially, T., Parallelism in Fast Fourier Transform Hardware, IEEE Transactions on Audio Electroacoustics, Vol. 21, No. 1, 1973.

[Hou87] Hou, Hsieh S., The Fast Hartley Transform Algorithm, IEEE Transactions on Computers, Vol. 36, No. 2, February 1987.

[Kaba86] Kabal, P. & Sayar, B., Performance of Fixed-Point FFT's: Rounding and Scaling Considerations, IEEE ICASSP 1986.

[Kane70] Kaneko, T. & Liu, B., Accumulation of Round-Off Error in Fast Fourier Transforms, J. Assoc. Computing Machinery, Vol. 17, No. 4, pp. 637-654, 1970.

[Kore81] Koren, I. A Reconfigurable and Fault-Tolerant VLSI Multiprocessor Array, Proceedings of the 8th International Symposium on Computer Architecture, Minneapolis, Minn, 1981.

[Kuma86] Kumaresan, R. & Gupta, P. K., Vector Radix Algorithm for a 2-D Discrete Hartley Transform, Proc. IEEE, Vol. 74, No. 5, May 1986.

[KUSK89] KUSKIN, J.,A Hardware Monitor for the MC68000, B.E.Thesis, Thayer School of Engineering, Dartmouth College, December 1989.

[Kwon86] Kwong, C. P., & Shiu, K. P., Structured Fast Hartley Transform Algorithms, IEEE Trans. ASSP, Vol. 34, No. 4, August 1986.

[Lamb86] Lamb, K., CMOS DSP building blocks adjust precision dynamically, Electronic Design, October 30, 1986, pp. 96-103.

[Land89] Landaeta, Dave & Menezes, Melwin, The Fast Hartley Transform on the Connection Machine, Thayer School of Engineering, Dartmouth College.

[LeNg89] Le-Ngoc, Tho & Vo, Minh Tue, Implementation and Performance of the Fast Hartley Transform, IEEE Micro, Vol. 9 , No. 5, October 1989, pp. 20 - 27.

[Lin88] Lin, X., Chan, T. F. & Karplus, W. J., The Fast Hartley Transform on the Hypercube Multiprocessors, University of California, Los Angeles, No. CSD-880011, Feb., 1988.

[Lind85] Linderman, Richard W., Chau, Paul M., Ku, Walter H. & Reusens, Peter P., CUSP: A 2µm CMOS Digital Signal Processor, IEEE Journal of Solid-State Circuits, Vol. 20, No. 3, June 1985.

[Marr86] Marrin, Ken, Six DSP processors tackle high-end signal processing applications, Computer Design, March 1, 1986, pp. 21 - 25.

[Mou88] Mou, Z.-J. & Duhamel, P., In-Place Butterfly-Style FFT of 2-D Real Sequences, IEEE Trans. ASSP Vol. 36, No. 10, October 1988, pp.1642-1650.

[Onei88] O’NEILL, MARK A., Faster Than Fast Fourier, Byte, April, 1988, pp. 293-300.

[oppe89] Oppenheim, Alan V. and Schafer, Ronald W. Discrete Time Signal Processing. Englewood Cliffs, New Jersey, Prentice Hall, Inc., 1989.

[Rabi75] Rabiner, Lawrence R. and Gold, Bernard. Theory and Application of Digital Signal Processing. Englewood Cliffs, New Jersey, Prentice Hall, Inc., 1975.

[Schw86] Schwartz, M., Schlappacasse, J. & Baskerville, G., Signal processor’s multiple memory buses shuttle data swiftly, Electronic Design, February 20, 1986, pp. 147-153.

[Shen88] SHEN, S., MAGAR, S., AGUILAR, R., LUIKUO, G., FLEMING, M., RISHAVY, K., MURPHY, K. & FURMAN, C., A High Performance CMOS Chipset for FFT Processors., Proceedings of the IEEE International Conference on Computer Design: VLSI In Computers and Processors, 1988, pp. 578 - 581.

[Sore85] Sorensen, H. K., Jones, D. L, Burrus, C. S. & Heideman, M. T., On Computing the Discrete Hartley Transform, IEEE Trans. ASSP, Vol. 33, No. 4, October 1985.

[Sore87] Sorensen, H. K., Jones, D. L, Heideman, M. T. & Burrus, C. S., Real-Valued Fast Fourier Transform Algorithms, IEEE Trans. ASSP, Vol. 35, No. 6, June 1987.

[Swar84] Swartzlander, E. E. Jr., Young, W. K. W. & Joseph, S. J., A Radix-4 Commutator for Fast Fourier Transform Processor Implementation, IEEE Journal of Solid-State Circuits, Vol. 19, No. 5, October 1984.

[TMC89] THINKING MACHINES CORPORATION, Connection Machine Technical Summary, Cambridge Massachusetts, 1989.

[Welc69] Welch, Peter D., A Fixed-Point Fast Fourier Transform Analysis, IEEE Transactions on Audio Electroacoustics, Vol. 17, No. 2, pp. 151-157, 1969.

[Welt85] Welten, F. P. J. M., Delaruelle, A., Van Wyk, F. J., Van Meerbergen, J. L., Schmid, J., Rinner, K., Van Eerdewijk, K. J. E. & Wittek, J. H., A 2-µm CMOS 10-MHz Microprogrammable Signal Processing Core With an On-Chip Multiport Memory Bank, IEEE Journal of Solid-State Circuits, Vol. 20, No. 3, June 1985.

[Zakh87] Zakhor, A. & Oppenheim, A. V., Quantization Errors in the Computation of the Discrete Hartley Transform, IEEE Trans. ASSP Vol. 35, No. 11, November 1987.

Appendix: Error Analysis

The following pages give simulated error analysis results for a 32-point maximum amplitude truncated cosine wave. We employ two programs: program A, a double-precision FHT algorithm, and program B, the FHT processor hardware emulator. Table A.1 shows the output of Program A for a 32-point, truncated cosine wave input sequence. Figure A.1 graphs the final sequence (last column).

Bit Reversal Stage 1 Stage 2 Stage 3 Stage 4 Final Sequence

------------ ---------- ---------- ---------- ---------- --------------

16383.0000 16383.0000 16383.0000 32766.0000 0.0000 0.0000

0.0000 16383.0000 16383.0000 39552.0608 -3258.7813 -3258.7813

0.0000 0.0000 16383.0000 32766.0000 9596.9392 9596.9392

0.0000 0.0000 16383.0000 16383.0000 16383.0000 16383.0000

16383.0000 16383.0000 16383.0000 0.0000 0.0000 0.0000

0.0000 16383.0000 16383.0000 -6786.0608 -24518.8922 -24518.8922

0.0000 0.0000 16383.0000 0.0000 -23169.0608 -23169.0608

0.0000 0.0000 16383.0000 16383.0000 16383.0000 16383.0000

-16383.0000 -16383.0000 -16383.0000 -32766.0000 65532.0000 65532.0000

0.0000 -16383.0000 -16383.0000 -39552.0608 82362.9029 82362.9029

0.0000 0.0000 -16383.0000 -32766.0000 55935.0608 55935.0608

0.0000 0.0000 -16383.0000 -16383.0000 16383.0000 16383.0000

-16383.0000 -16383.0000 -16383.0000 0.0000 0.0000 0.0000

0.0000 -16383.0000 -16383.0000 6786.0608 10946.7706 10946.7706

0.0000 0.0000 -16383.0000 0.0000 23169.0608 23169.0608

0.0000 0.0000 -16383.0000 -16383.0000 16383.0000 16383.0000

0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

0.0000 0.0000 0.0000 0.0000 0.0000 -3258.7813

0.0000 0.0000 0.0000 0.0000 0.0000 9596.9392

0.0000 0.0000 0.0000 0.0000 0.0000 16383.0000

0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

0.0000 0.0000 0.0000 0.0000 0.0000 -24518.8922

0.0000 0.0000 0.0000 0.0000 0.0000 -23169.0608

0.0000 0.0000 0.0000 0.0000 0.0000 16383.0000

0.0000 0.0000 0.0000 0.0000 0.0000 65532.0000

0.0000 0.0000 0.0000 0.0000 0.0000 82362.9029

0.0000 0.0000 0.0000 0.0000 0.0000 55935.0608

0.0000 0.0000 0.0000 0.0000 0.0000 16383.0000

0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

0.0000 0.0000 0.0000 0.0000 0.0000 10946.7706

0.0000 0.0000 0.0000 0.0000 0.0000 23169.0608

0.0000 0.0000 0.0000 0.0000 0.0000 16383.0000

Table A.1 FHT of Maximum-Amplitude Truncated Cosine Wave: Program A

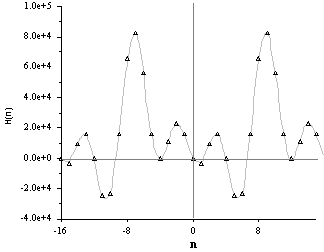
Figure A.1 FHT of 32-Point Truncated Cosine Wave

Table A.2 lists the output of Program B using the same input sequence. Note the order in which the output sequence must be read and the value of the exponent register.

Assuming that the double-precision results of Program A are exact, we can calculate the signal-to-noise ratio of the processor’s fixed-point output for a maximum-amplitude, truncated cosine wave. Following the procedure outlined in previous sections, we find that the SNR of our output sequence is 71 dB. Given that the data began with 14 bits of precision (excluding the sign bit), this corresponds to an average decrease in SNR of 0.44 bits per stage.

n z(n) + e(n) z(n) e(n) [z(n) - avg(z)]² [e(n) - avg(e)]²

0 -16 0.0000 -16.0000 2.6840E+08 64.00000

1 -3280 -3258.7813 -21.2187 3.8580E+08 174.73403

2 9584 9596.9392 -12.9392 4.6051E+07 24.39570

3 16368 16383.0000 -15.0000 3.3087E-24 49.00000

4 0 0.0000 0.0000 2.6840E+08 64.00000

5 -24528 -24518.8922 -9.1078 1.6730E+09 1.22722

6 -23168 -23169.0608 1.0608 1.5644E+09 82.09810

7 16368 16383.0000 -15.0000 3.3087E-24 49.00000

8 65520 65532.0000 -12.0000 2.4156E+09 16.00000

9 82368 82362.9029 5.0971 4.3533E+09 171.53403

10 55920 5935.0608 -15.0608 1.5644E+09 49.85490

11 16384 16383.0000 1.0000 3.3087E-24 81.00000

12 0 0.0000 0.0000 2.6840E+08 64.00000

13 10944 10946.7706 -2.7706 2.9553E+07 27.34662

14 23168 23169.0608 -1.0608 4.6051E+07 48.15250

15 16368 16383.0000 -15.0000 3.3087E-24 49.00000

16 -16 0.0000 -16.0000 2.6840E+08 64.00000

17 -3280 -3258.7813 -21.2187 3.8580E+08 174.73403

18 9584 9596.9392 -12.9392 4.6051E+07 24.39570

19 16368 16383.0000 -15.0000 3.3087E-24 49.00000

20 0 0.0000 0.0000 2.6840E+08 64.00000

21 -24528 -24518.8922 -9.1078 1.6730E+09 1.22722

22 -23168 -23169.0608 1.0608 1.5644E+09 82.09810

23 16368 16383.0000 -15.0000 3.3087E-24 49.00000

24 65520 65532.0000 -12.0000 2.4156E+09 16.00000

25 82368 82362.9029 5.0971 4.3533E+09 171.53403

26 55920 55935.0608 -15.0608 1.5644E+09 49.85490

27 16384 16383.0000 1.0000 3.3087E-24 81.00000

28 0 0.0000 0.0000 2.6840E+08 64.00000

29 10944 10946.7706 -2.7706 2.9553E+07 27.34662

30 23168 23169.0608 -1.0608 4.6051E+07 48.15250

31 16368 16383.0000 -15.0000 3.3087E-24 49.00000

Avg.: 16375 16383.0000 -8.0000 - -

Sum/N-1 (s²): - - 8.3118E+08 65.50601

Table A.2 Calculating Signal-to-Noise Ratio

---

^[1] The complex FFT can be used to simultaneously compute the transform of 2 real-valued sequences. However, the two resulting transforms are scrambled, requiring a fair amount of post-processing to separate the two transforms.

^[2]Here and throughout the paper, logN denotes log₂N.

^[3] Performance benchmarks for several DSP processors and dedicated FFT processors are given in section 5.

^[4] It is interesting to note that the real-valued FFT algorithm also exhibits the retrograde addressing property and the same butterfly structure of Figure 1.5. The inverse transform, however, has a different butterfly structure.

^[5] The effects of scaling may offset any error introduced by roundoff as the “noisy” bits are shifted out and discarded. Some implementations round the scaled data according to the value of the discarded bit. If the shifted bit was ‘0’, no error occurs, and the bit is discarded. If the shifted bit was ‘1’, then one is added to the data after shifting. Thus 3 shifted by 1 bit and rounded gives 2. Scaling the data in this way produces a mild improvement in the output signal-to-noise ratio at the cost of a more complex BCU.

^[6] If the data are to be involved in another transform (i.e. IFHT), the data must be readjusted to within [-2¹⁴,2¹⁴-1]